Ongoing Projects
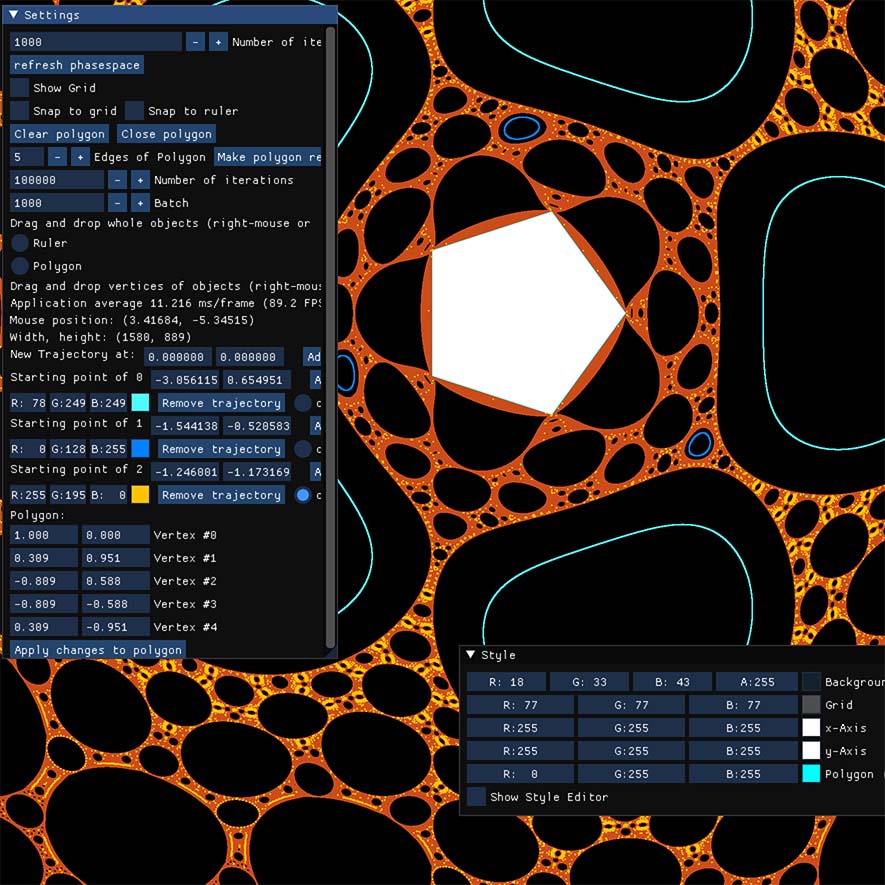
Outer Length Billiards
[Fabian Lander, David Seyboldt, Peter Albers]
To investigate the discrete dynamical system of outer length billiards in the planar case of polygons, we developed an interactive program to simulate the system. This software is capable of simulating multiple trajectories simultaneously within a single polygon. To differentiate between these trajectories, each can be assigned a different color. Furthermore, we utilize fragment shader programs [read more]
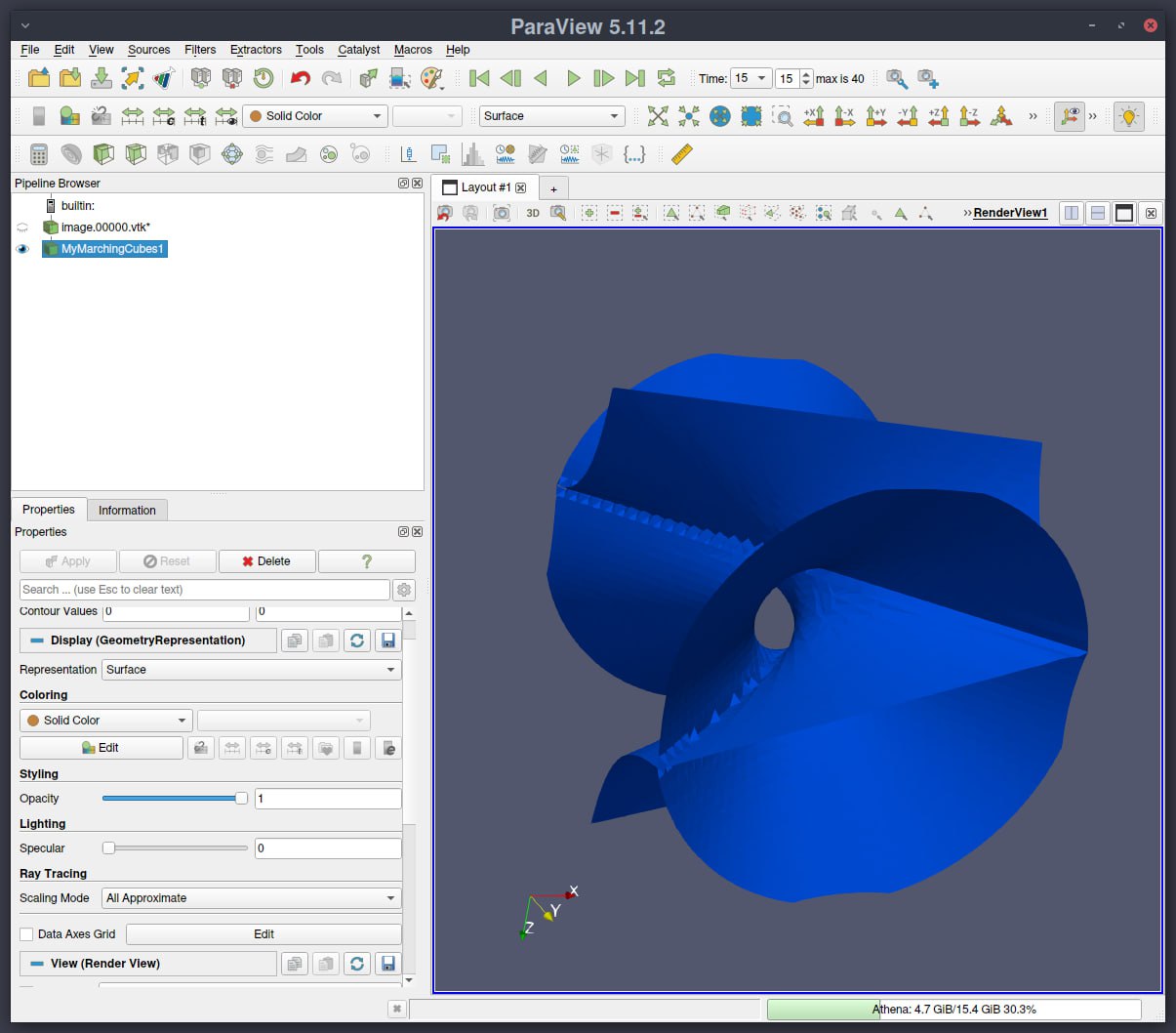
Paraview Installer
This tool installs the open-source multiple-platform application ParaView for interactive, scientific visualization, together with CRC/TRR 191 related plugins and supports automatic updates when new plugins are published.
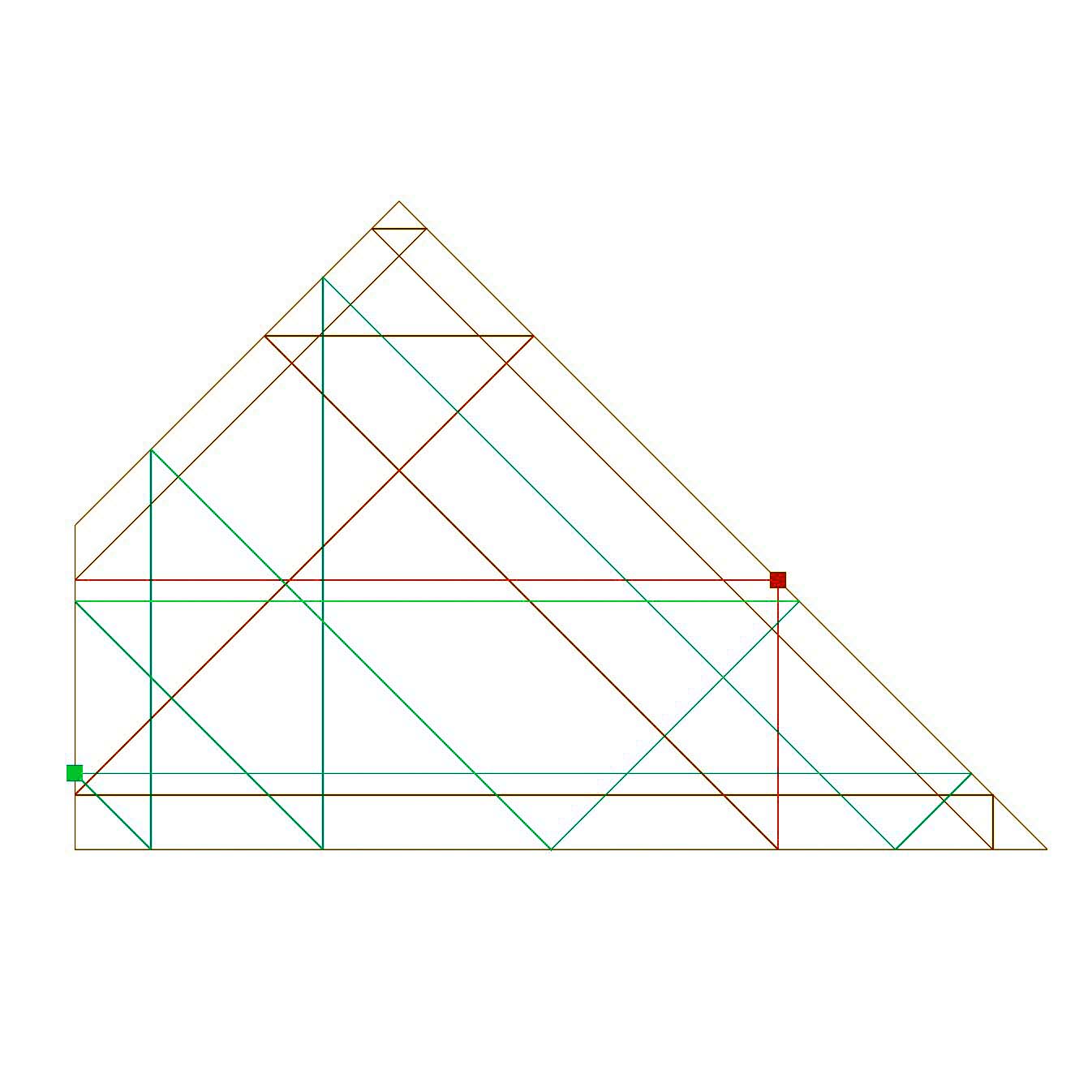
Polygonal Symplectic Billiards
[Fabian Lander, Jannik M. Westermann, Peter Albers]
We are investigating the discrete dynamical system of symplectic billiards in the planar case of polygons. We are looking at the problems from a two-table perspective that subsumes the single table perspective. The project has involved a theoretical and a programming component. The theoretical component included stating and proving new theorems concerning the existence of periodic orbits and [read more]
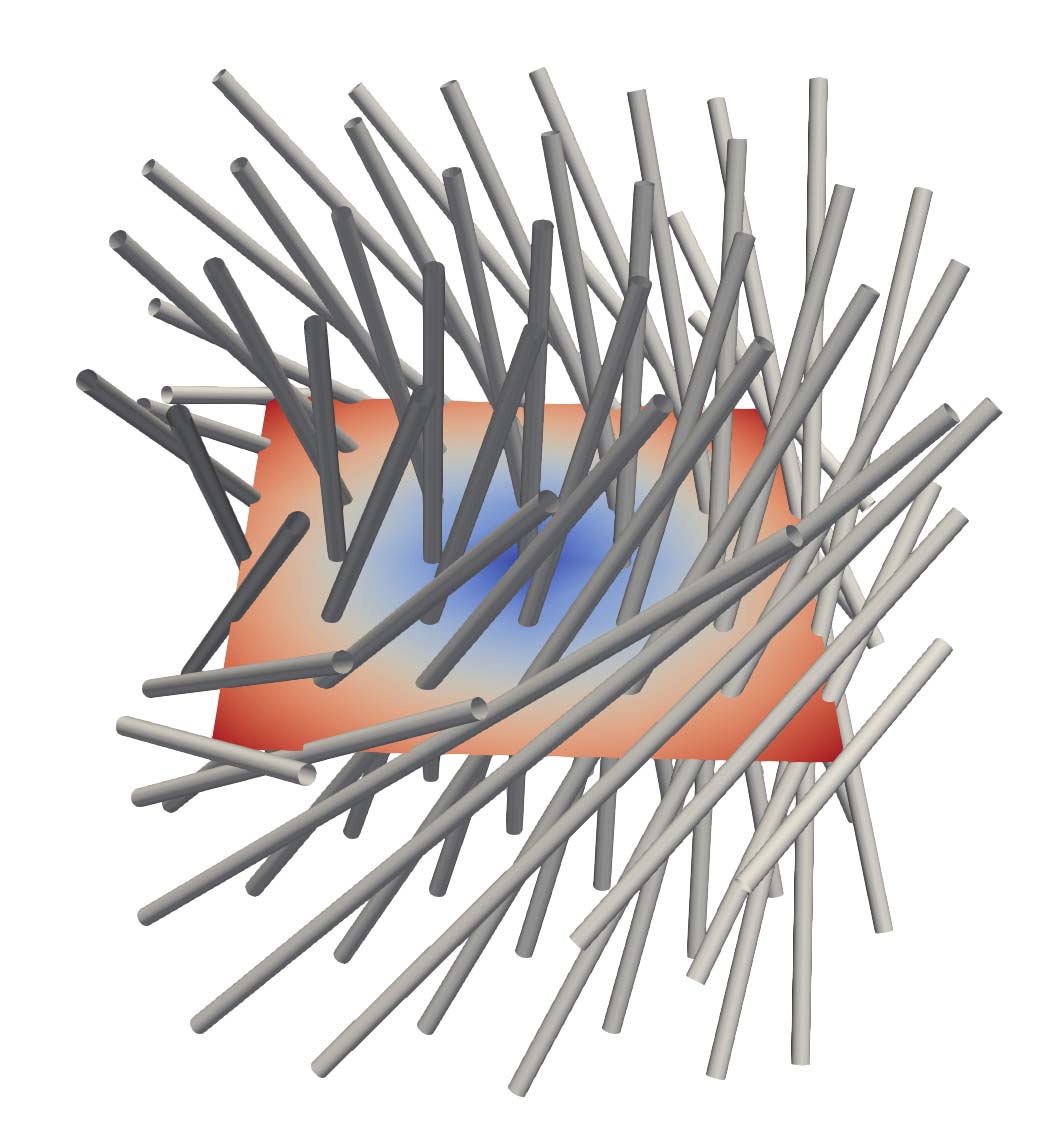
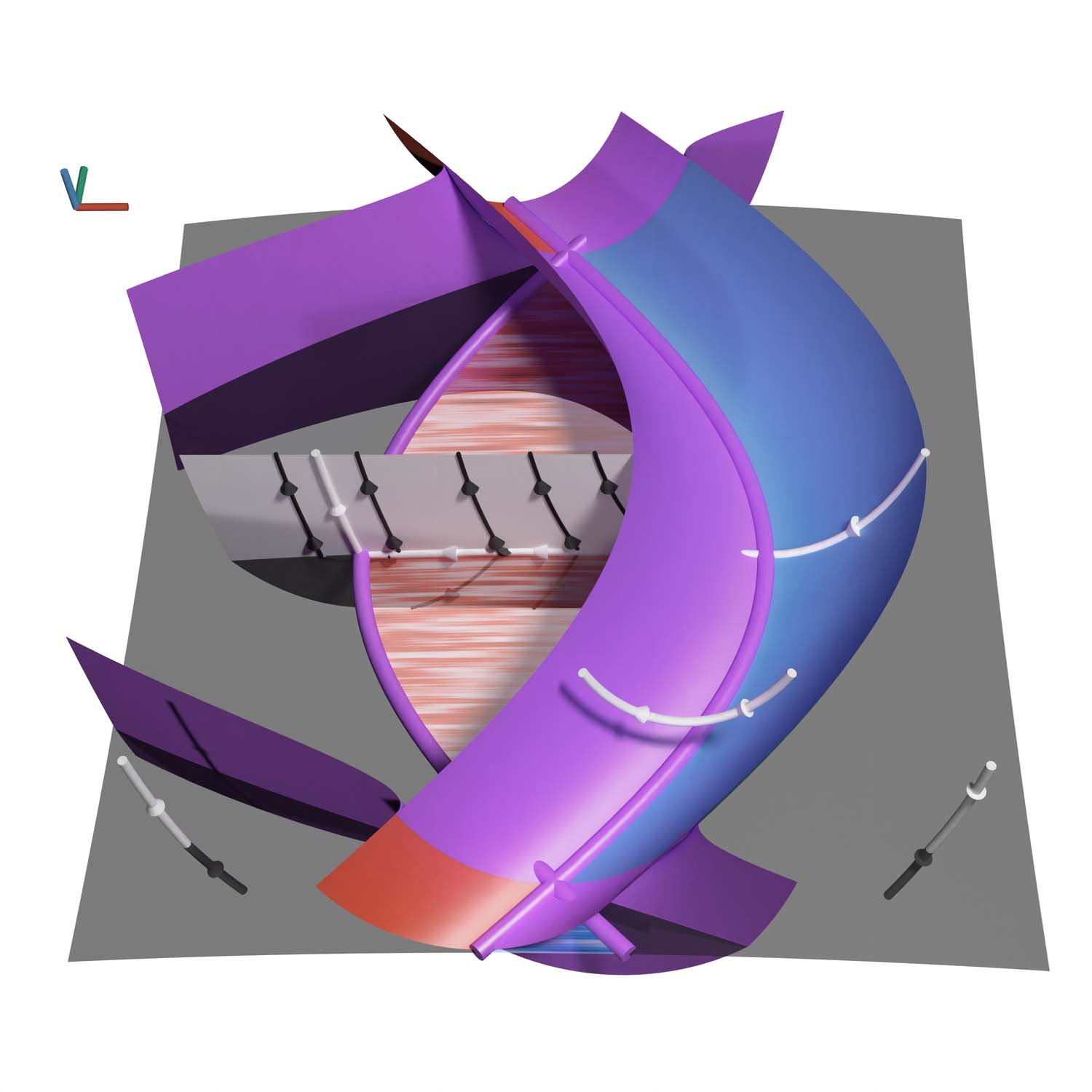
Visualization of Line and Skew Fibrations
In the realm of geometric analysis, skew fibrations—where non-parallel fibers within a line fibration do not intersect—play a crucial role. This project focuses on extracting subregions from discretized data in R³ containing such skew fibrations. We propose a methodology combining computational geometry and data visualization techniques to identify and visualize these skew fibrations amidst [read more]
Web-Based Flow Visualization in Quotient Space and 𝕊³
We present a readily accessible web-based interactive system for ray casting-based flow visualization in quotient spaces and 𝕊³. It is the result of a long-term close collaboration with researchers from symplectic geometry, and focuses on accessibility, flexibility, and provenance. By storing its state in URLs and providing a version-aware mechanism to link from images in PDFs to the online tool [read more]
Completed Projects (Newest First)
Visualization of Discontinuous Vector Field Topology
[Egzon Miftari, Daniel Durstewitz, Filip Sadlo](completed: 2024-01)
This paper extends the concept and the visualization of vector field topology to vector fields with discontinuities. We address the non-uniqueness of flow in such fields by introduction of a time-reversible concept of equivalence. This concept generalizes streamlines to streamsets and thus vector field topology to discontinuous vector fields in terms of invariant streamsets. We identify [read more]
Local Extraction of 3D Time-Dependent Vector Field Topology
[Lutz Hofmann, Filip Sadlo](completed: 2021-06-29)
We present an approach to local extraction of 3D time-dependent vector field topology. In this concept, Lagrangian coherent structures, which represent the separating manifolds in time-dependent transport, correspond to generalized streak manifolds seeded along hyperbolic path surfaces (HPSs). Instead of expensive and numerically challenging direct computation of the HPSs by intersection of [read more]
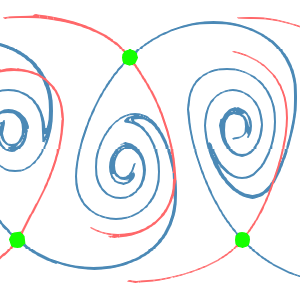
Extraction of Distinguished Hyperbolic Trajectories for 2D Time-Dependent Vector Field Topology
[Lutz Hofmann, Filip Sadlo](completed: 2020-07-18)
This paper does two main contributions to 2D time-dependent vector field topology. First, we present a technique for robust, accurate, and efficient extraction of distinguished hyperbolic trajectories (DHT), the generative structures of 2D time-dependent vector field topology. It is based on refinement of initial candidate curves. In contrast to previous approaches, it is robust because the [read more]