Ongoing Projects
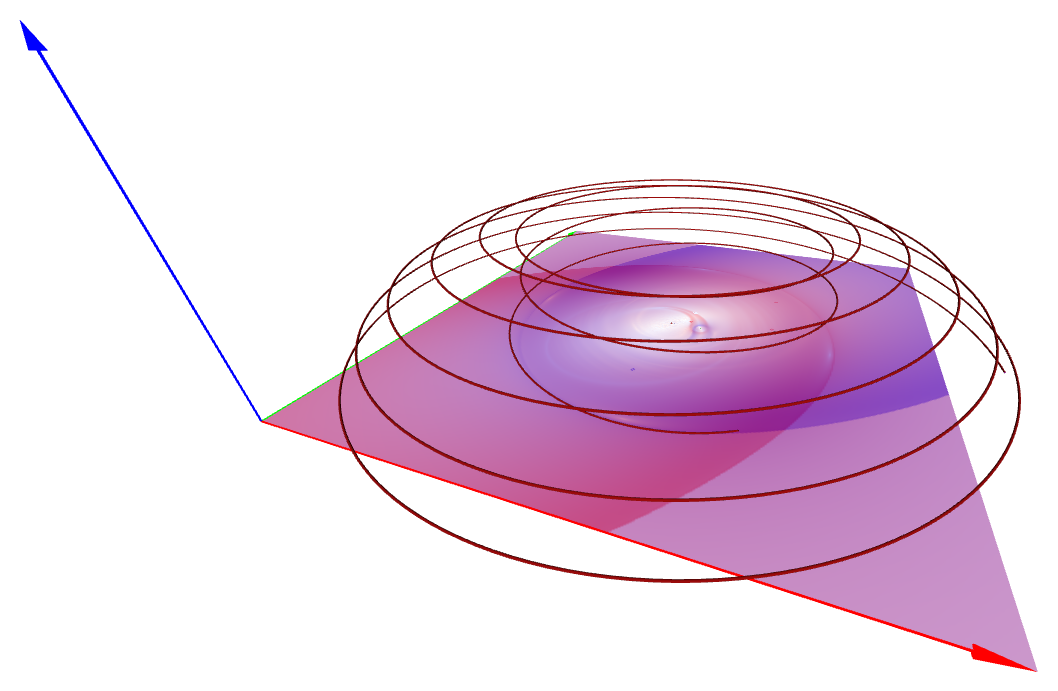
Visualization of CR3BP Return Maps [Practical]
Work in progress. This tool allows interactive exploration of return maps in the Circular Restricted Three-Body Problem.
Completed Projects (Newest First)
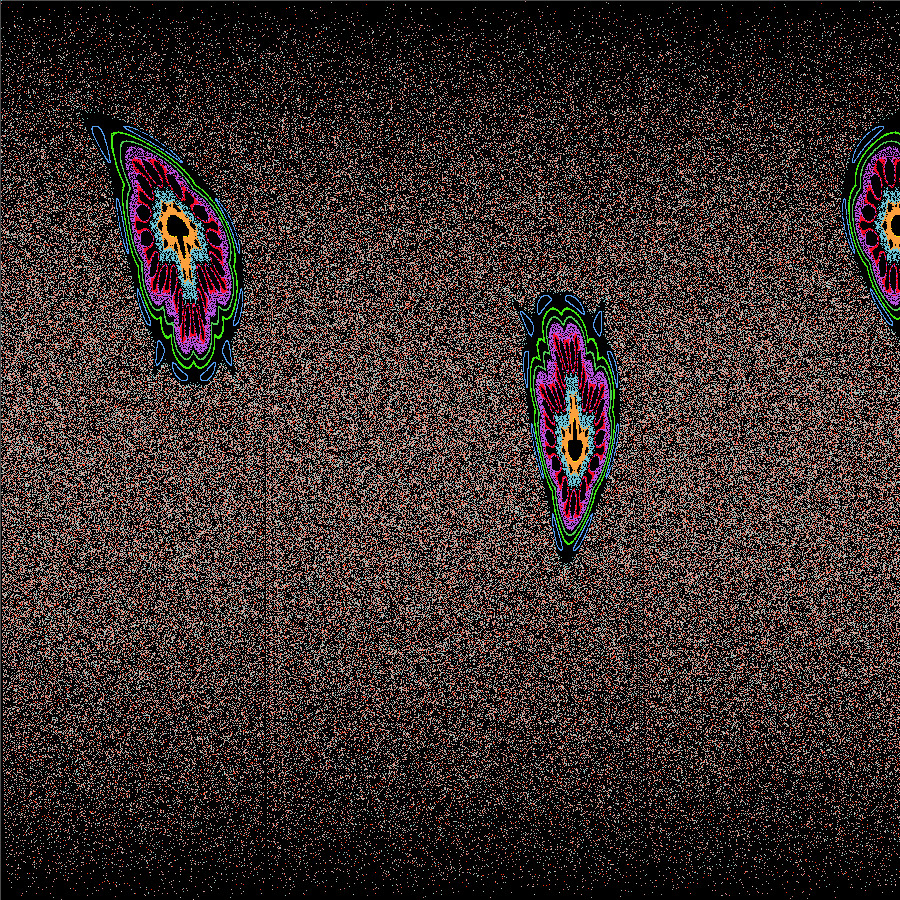
Polygonal Inverse Magnetic Billiards [Practical]
[Katrin Weigand, David Seyboldt](completed: 2023-12-06)
This web-based tool allows the simulation of inverse magnetic billiards, regular billiards and symplectic billiards on polygonal tables in 2D. The program includes a shader-based flow map and FTLE for each billiard type. Furthermore, the phase space can be automatically filled with trajectories.
Visualization of Symplectic and Euclidean Billiards in Polygons and Bézier Curves [Practical]
[Denise Becker, Robin Hoffmann](completed: 2023-12-06)
The aim of our previous work, “Visualization of Symplectic and Euclidean Billiards in Polygons”, was to explore and visualize Euclidean and Symplectic billiards in convex and non-convex polygons. This report focuses on integrating more complex functionalities to deepen the research and understanding of mathematical billiards. The extensions include the introduction of Bézier curves instead of [read more]
Visualization of Overtwisted Disks in R³ [Master Thesis]
[Marco Kowalzik](completed: 2023-03-30)
This thesis is about the numerical extraction of overtwisted disks in contact structures
in R³. Overtwisted disks play an important role in contact geometry as their
existence distinguishes two different kinds of contact structures, namely the overtwisted
and the tight contact structures. On the other side they are also useful for
the visualization of overtwisted contact structures, especially in [read more]
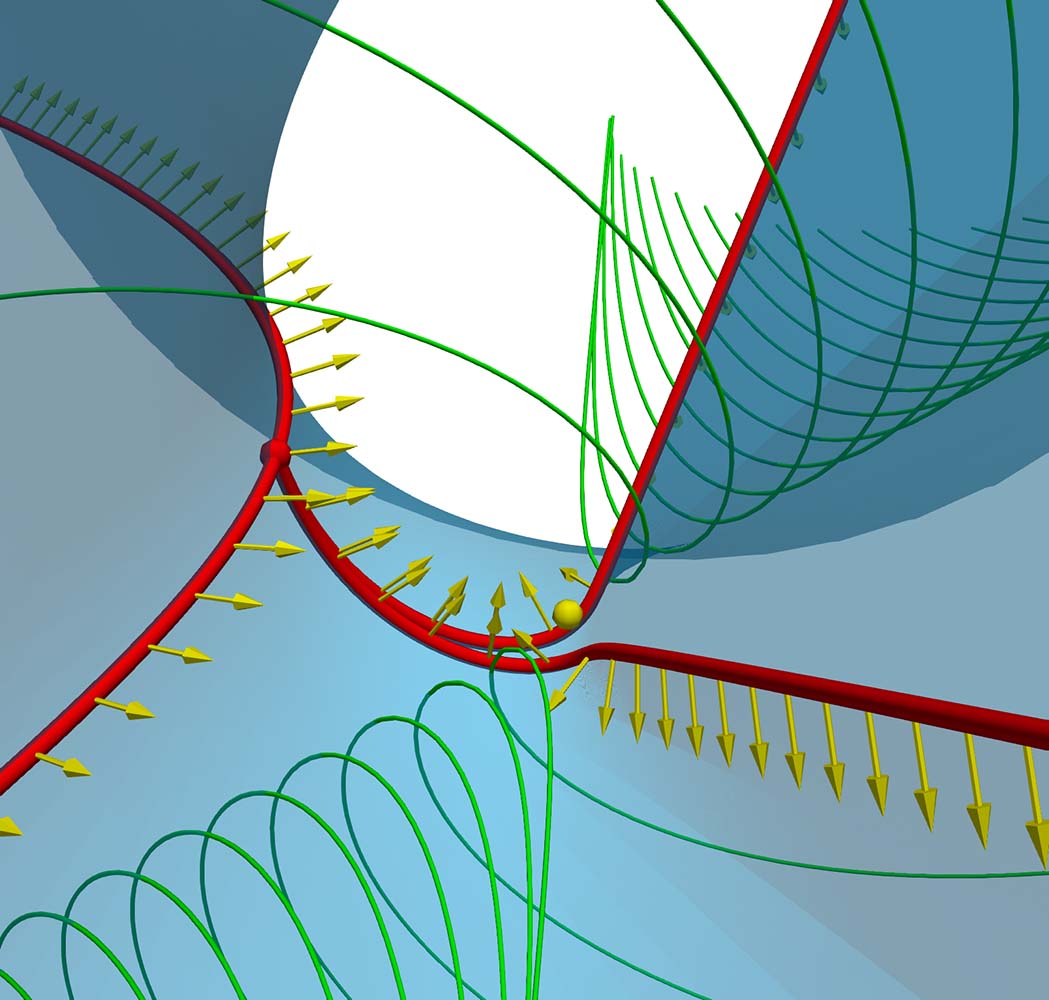
Visualization of Surfaces of Section [Master Thesis]
[Joshua Bossert](completed: 2022-12-06)
In the last decades, many different methods for vector field visualization have been introduced. One technique is the visualization of flow maps. It maps a point in the domain to a position reached by tracing a characteristic line, like a streamline, through the vector field. These maps are represented on two-dimensional surfaces. Therefore, three-dimensional fields have to be reduced to a [read more]
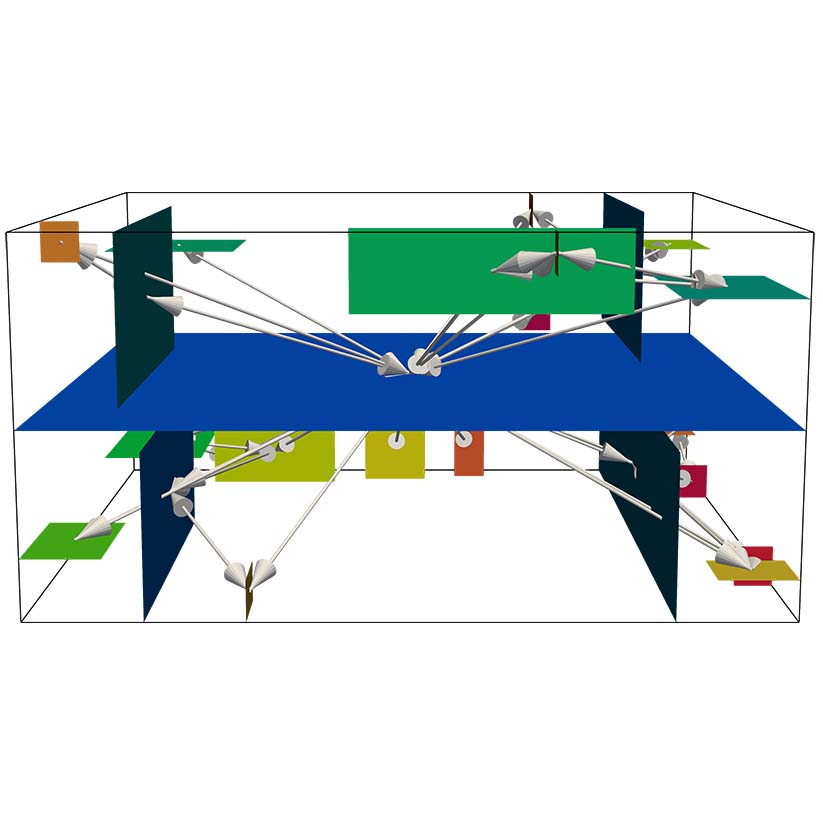
Features in Plane Fields [Master Thesis]
[Clara Hartmann](completed: 2022-11-10)
This thesis introduces and examines features of two-plane fields in three dimensions. In a plane field, each position of a three-manifold is associated with a tangential two-dimensional plane. In the past, plane fields underwent a lack of attention in visualisation and research. In this work, two main features are identified and proposed for visualisation. The first feature identifies positions [read more]
Visualization of Integral Curves in Plane Fields [Bachelor Thesis]
[Leonard Marks](completed: 2022-09-20)
This thesis explores methods to visualise contact geometries, which are interpreted as plane field, by using curves related to properties like curvature and torsion, as well as using vector field properties like the eigenvectors of the Jacobian matrix. First we introduce some mathematical fundamentals of differential geometry which are needed to understand and construct the curves introduced. As [read more]
Visualization of Planefields [Master Thesis]
[Sebastian Hegmann](completed: 2020-11-28)
Within the master thesis a framework for the analysis of plane fields will be developed. Using a particle simulation, these fields will be visualized and afterwards examined for properties. Due to the large-scale computational problem, the calculations are performed on the graphics card using CUDA. The introduction of a new approach should provide further insights into the behavior of general [read more]