Visualization of Surfaces of Section
Abstract
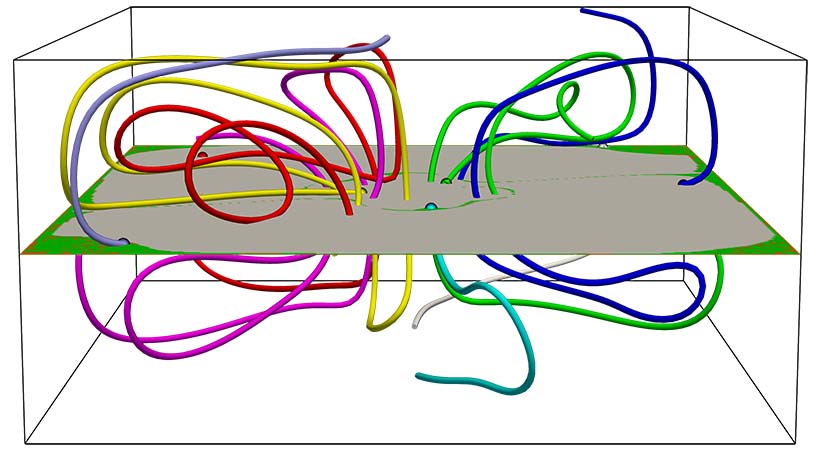
In the last decades, many different methods for vector field visualization have been introduced. One technique is the visualization of flow maps. It maps a point in the domain to a position reached by tracing a characteristic line, like a streamline, through the vector field. These maps are represented on two-dimensional surfaces. Therefore, three-dimensional fields have to be reduced to a two-dimensional representation which is often done by using surfaces of section. These are sections of the vector field domain on which the flow map is evaluated. The challenging task is to place these surfaces so that the map on it indicates the domain's topology.
In this thesis, we introduce a definition for a set of surfaces of section~$S$ that covers the entire vector field domain with streamlines seeded on these surfaces. We furthermore define a non-redundant set of surfaces of section~$S^*$ that additionally fulfills the property that every point in the domain is covered by exactly one streamline seeded on a surface in~$S^*$.
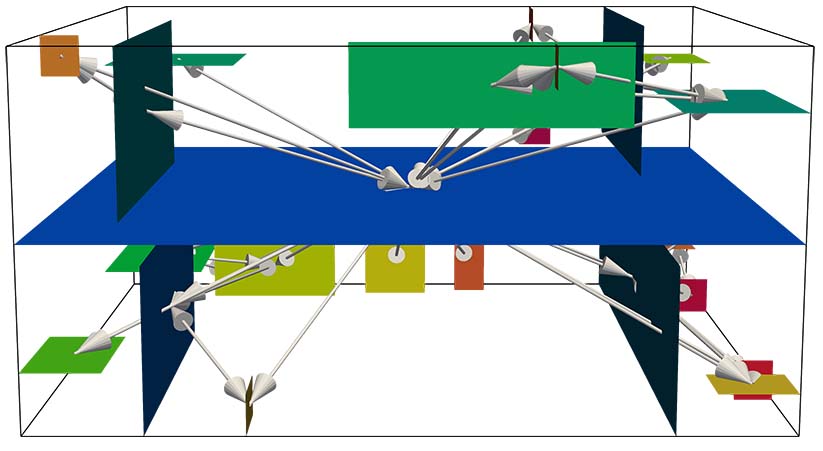
We present a framework consisting of a greedy approach for extracting the surfaces of section~$S$ and~$S^*$ and various representations on these surfaces. Therefore, we introduce the concept of a first intersection event map for each streamline seeded on the surfaces of section. This flow map maps every point on the surfaces to the first intersection point with another surface of section. If the streamline is not intersecting with any surface, the point of its integration termination is considered the first intersection event. This can be the point where the streamline leaves the domain, stagnates, or is terminated due to reaching the maximum propagation of the integration.
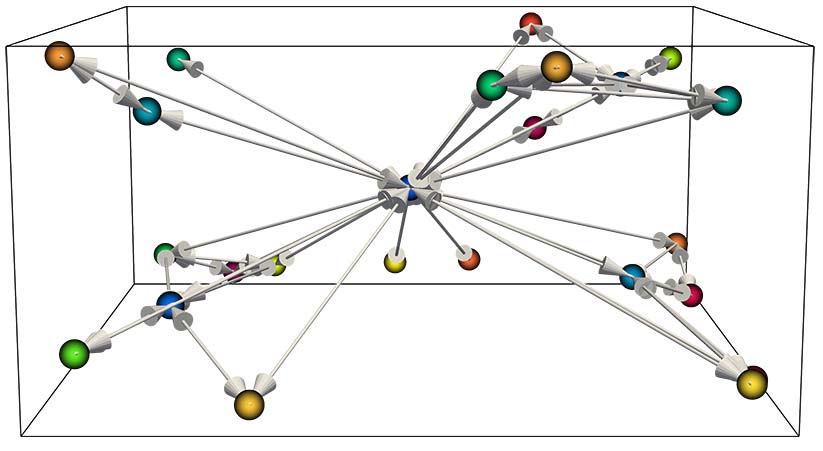
With the first intersection event map, we introduce representations for the surfaces of section to depict the entire vector field topology. First, we directly map the event point to RGB colors to show the overall structure of the flow map. Then, we use the finite-time Lyapunov exponent (FTLE) to highlight regions where the streamlines seeded, have similar behavior. We support these representations with chosen trajectories in the form of seeded streamlines or arrows pointing from the seeding point to the point of the first intersection event. To trace the flow, we introduce a graph representation that illustrates the connectivity of the surfaces of section via the streamlines seeded on them.
We evaluate our approach by applying three synthetic data sets and one sampled data set. With this examination, we demonstrate the capabilities and limitations of the algorithm to extract the surfaces of section~$S$ and~$S^*$. Furthermore, we show the usability of the introduced representations to understand the vector field topology. Finally, we discuss the framework's potential for extensions and enhancements in future work.
Links
In this thesis, we introduce a definition for a set of surfaces of section~$S$ that covers the entire vector field domain with streamlines seeded on these surfaces. We furthermore define a non-redundant set of surfaces of section~$S^*$ that additionally fulfills the property that every point in the domain is covered by exactly one streamline seeded on a surface in~$S^*$.
We present a framework consisting of a greedy approach for extracting the surfaces of section~$S$ and~$S^*$ and various representations on these surfaces. Therefore, we introduce the concept of a first intersection event map for each streamline seeded on the surfaces of section. This flow map maps every point on the surfaces to the first intersection point with another surface of section. If the streamline is not intersecting with any surface, the point of its integration termination is considered the first intersection event. This can be the point where the streamline leaves the domain, stagnates, or is terminated due to reaching the maximum propagation of the integration.
With the first intersection event map, we introduce representations for the surfaces of section to depict the entire vector field topology. First, we directly map the event point to RGB colors to show the overall structure of the flow map. Then, we use the finite-time Lyapunov exponent (FTLE) to highlight regions where the streamlines seeded, have similar behavior. We support these representations with chosen trajectories in the form of seeded streamlines or arrows pointing from the seeding point to the point of the first intersection event. To trace the flow, we introduce a graph representation that illustrates the connectivity of the surfaces of section via the streamlines seeded on them.
We evaluate our approach by applying three synthetic data sets and one sampled data set. With this examination, we demonstrate the capabilities and limitations of the algorithm to extract the surfaces of section~$S$ and~$S^*$. Furthermore, we show the usability of the introduced representations to understand the vector field topology. Finally, we discuss the framework's potential for extensions and enhancements in future work.