Features in Plane Fields
Abstract
This thesis introduces and examines features of two-plane fields in three dimensions. In a plane field, each position of a three-manifold is associated with a tangential two-dimensional plane. In the past, plane fields underwent a lack of attention in visualisation and research. In this work, two main features are identified and proposed for visualisation. The first feature identifies positions that are passed by an integral curve with vanishing curvature. The second feature identifies regions of extreme curvature of the plane field.
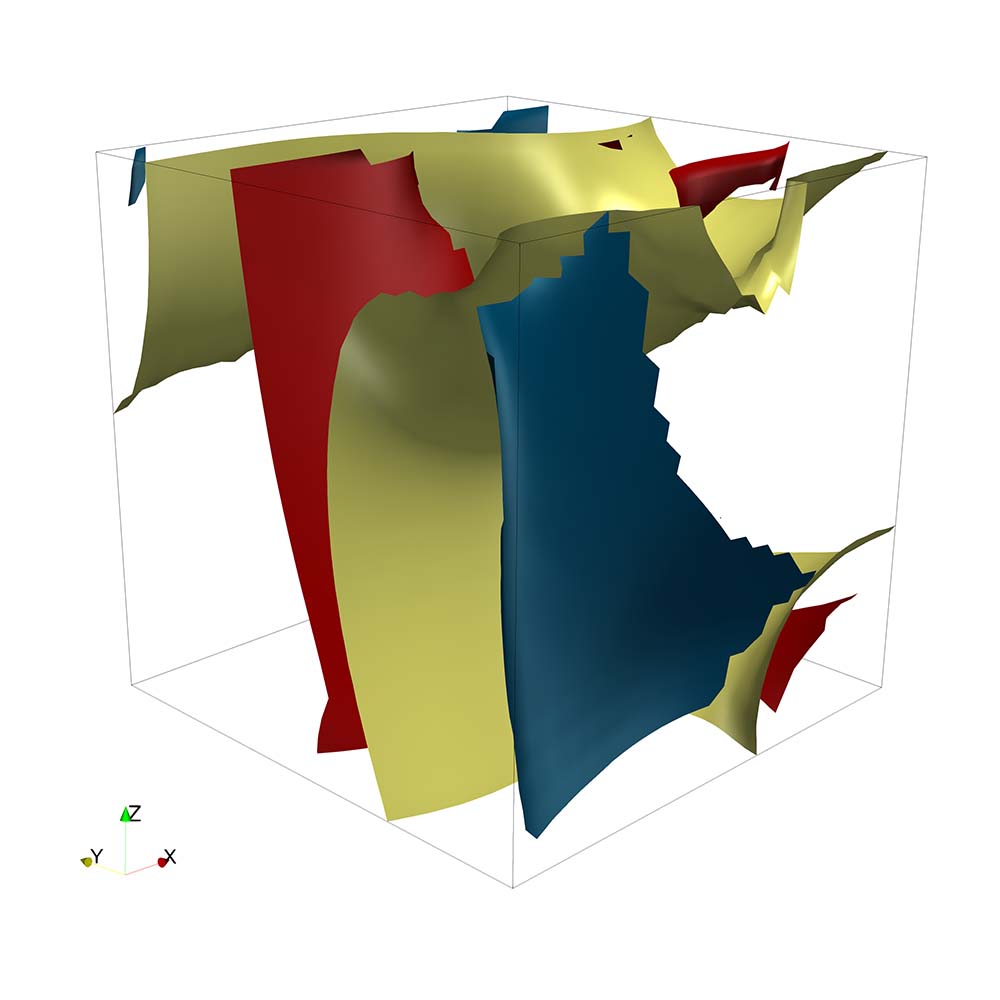
The first feature bases on a specific type of integral curves through a plane field, called natural curves. The feature consists of all positions of the three-manifold that are passed by at least one natural curve that has vanishing curvature at this position. It turns out that the positions of the feature describe solution surfaces, which are called the zero-curvature surfaces. Analogous to vortex core lines and attachment lines in three-dimensional vector fields, each position can be classified concerning the movement of the natural curves in the neighbourhood. This thesis introduces an approach for extraction of these zero-curvature surfaces, which is based on the dependent vectors operator presented by Hofmann and Sadlo.
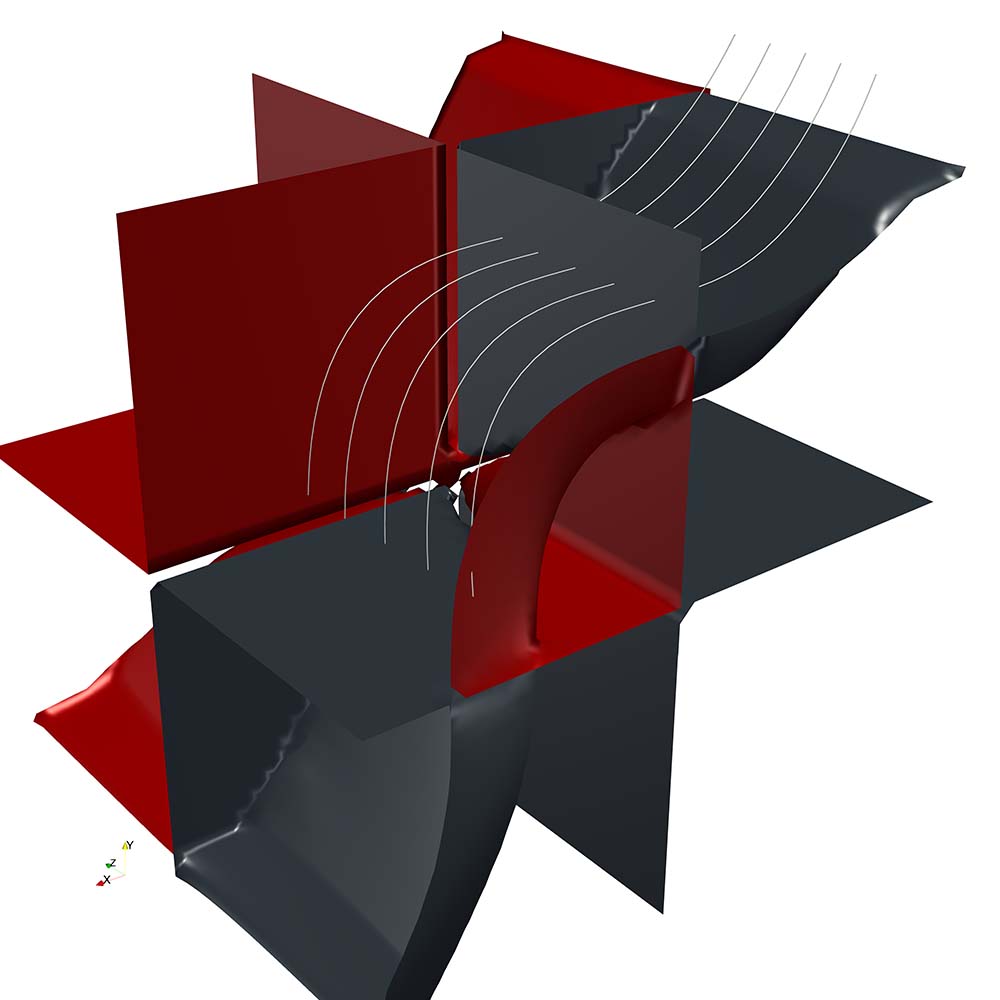
To convey the overall structure of plane fields, we generalise the concept of curvature ridges and valleys to plane fields, which specifies the second feature. Curvature ridges and valleys represent positions of local minima and maxima of the principal curvature. Thereby, positions of strong or weak variation of the tangent planes as well as positions where the integral curves of the plane field have high or low curvature are identified. An approach for extraction of these feature surfaces is introduced. The approach is based on curvature ridge extraction of surface meshes introduced by Hildebrandt, Polthier, and Wardetzky. For evaluation and discussion of the two features, the presented approaches are applied to synthetic data as well as to more complex simulated data.
Links
The first feature bases on a specific type of integral curves through a plane field, called natural curves. The feature consists of all positions of the three-manifold that are passed by at least one natural curve that has vanishing curvature at this position. It turns out that the positions of the feature describe solution surfaces, which are called the zero-curvature surfaces. Analogous to vortex core lines and attachment lines in three-dimensional vector fields, each position can be classified concerning the movement of the natural curves in the neighbourhood. This thesis introduces an approach for extraction of these zero-curvature surfaces, which is based on the dependent vectors operator presented by Hofmann and Sadlo.
To convey the overall structure of plane fields, we generalise the concept of curvature ridges and valleys to plane fields, which specifies the second feature. Curvature ridges and valleys represent positions of local minima and maxima of the principal curvature. Thereby, positions of strong or weak variation of the tangent planes as well as positions where the integral curves of the plane field have high or low curvature are identified. An approach for extraction of these feature surfaces is introduced. The approach is based on curvature ridge extraction of surface meshes introduced by Hildebrandt, Polthier, and Wardetzky. For evaluation and discussion of the two features, the presented approaches are applied to synthetic data as well as to more complex simulated data.